Introduction to Sets

Forget everything you know about numbers.

In fact, forget you even know what a number is.

This is where mathematics starts.

Instead of math with numbers, we will at present call up about math with "things".

Definition

What is a set up? Well, simply put, it's a collection.

First we specify a mutual property among "things" (we define this give-and-take later) and then we gather upward all the "things" that have this mutual belongings.

set of clothes

For example, the items you lot wear: hat, shirt, jacket, pants, and and then on.

I'm sure y'all could come up with at least a hundred.

This is known equally a set up.

Or another example is types of fingers.

This set up includes index, middle, ring, and pinky.

 set of fingers

So information technology is just things grouped together with a certain belongings in common.

Notation

There is a fairly simple notation for sets. We simply listing each element (or "member") separated by a comma, so put some curly brackets effectually the whole thing:

Set Notation

The curly brackets { } are sometimes called "set brackets" or "braces".

This is the notation for the 2 previous examples:

{socks, shoes, watches, shirts, ...}
{index, middle, ring, pinky}

Notice how the start example has the "..." (3 dots together).

The three dots ... are chosen an ellipsis, and mean "continue on".

So that means the showtime example continues on ... for infinity.

(OK, there isn't really an infinite amount of things you could wear, but I'one thousand non entirely sure virtually that! After an hour of thinking of different things, I'm still not sure. So let's only say it is infinite for this example.)

So:

  • The kickoff set {socks, shoes, watches, shirts, ...} nosotros call an space set,
  • the second set {alphabetize, centre, band, pinky} we phone call a finite set.

But sometimes the "..." can exist used in the eye to salvage writing long lists:

Instance: the set of messages:

{a, b, c, ..., x, y, z}

In this case information technology is a finite set (at that place are just 26 messages, right?)

Numerical Sets

So what does this have to practice with mathematics? When we define a set, all we take to specify is a common characteristic. Who says we tin can't practise so with numbers?

Set up of even numbers: {..., −4, −two, 0, 2, 4, ...}
Fix of odd numbers: {..., −3, −i, 1, three, ...}
Prepare of prime numbers: {2, 3, 5, 7, 11, xiii, 17, ...}
Positive multiples of 3 that are less than 10: {iii, half dozen, nine}

And so on. We tin can come upward with all different types of sets.

We can besides define a ready past its properties, such as {x|x>0} which means "the set of all x's, such that x is greater than 0", see Fix-Builder Notation to learn more.

And we tin have sets of numbers that have no common belongings, they are just defined that manner. For example:

{two, 3, half dozen, 828, 3839, 8827}
{4, 5, vi, 10, 21}
{ii, 949, 48282, 42882959, 119484203}

Are all sets that I only randomly banged on my keyboard to produce.

Why are Sets Important?

Sets are the central holding of mathematics. Now as a word of alert, sets, by themselves, seem pretty pointless. But it'south simply when we apply sets in dissimilar situations do they become the powerful building block of mathematics that they are.

Math tin can get amazingly complicated quite fast. Graph Theory, Abstract Algebra, Real Analysis, Complex Assay, Linear Algebra, Number Theory, and the listing goes on. Only there is one affair that all of these share in common: Sets .

Universal Set

star

At the start nosotros used the discussion "things" in quotes.

Nosotros call this the universal set. It's a set that contains everything. Well, not exactly everything. Everything that is relevant to our question.

various integers

In Number Theory the universal set is all the integers, as Number Theory is merely the report of integers.
various reals

Simply in Calculus (also known as real analysis), the universal gear up is almost always the existent numbers.
various complex numbers And in circuitous assay, you guessed it, the universal set is the complex numbers.

Some More Notation

A= {a,...} When talking about sets, information technology is fairly standard to employ Capital Letters to represent the gear up, and lowercase messages to represent an element in that set.

So for example, A is a fix, and a is an element in A. Aforementioned with B and b, and C and c.

Now yous don't have to listen to the standard, you tin use something like grand to represent a fix without breaking any mathematical laws (watch out, you can get π years in math jail for dividing by 0), merely this note is pretty nice and easy to follow, so why not?

As well, when nosotros say an element a is in a fix A, we use the symbol element symbol to show it.
And if something is non in a set use not element symbol.

Example: Set A is {ane,2,3}. Nosotros can run across that 1 element symbol A, but 5 not element symbol A

Equality

Two sets are equal if they take precisely the same members. Now, at first glance they may not seem equal, then we may accept to examine them closely!

Example: Are A and B equal where:

  • A is the set whose members are the first four positive whole numbers
  • B = {4, 2, i, 3}

Permit's check. They both contain 1. They both incorporate 2. And iii, And 4. And we have checked every element of both sets, so: Yes, they are equal!

And the equals sign (=) is used to prove equality, so we write:

A = B

Example: Are these sets equal?

  • A is {1, 2, iii}
  • B is {iii, 1, two}

Yeah, they are equal!

They both comprise exactly the members 1, 2 and 3.

It doesn't matter where each fellow member appears, so long every bit information technology is there.

subset

Subsets

When nosotros define a set, if we accept pieces of that set, we can form what is called a subset.

Example: the ready {1, 2, three, 4, v}

A subset of this is {1, ii, 3}. Another subset is {iii, four} or fifty-fifty some other is {1}, etc.

Just {one, half-dozen} is non a subset, since it has an element (6) which is not in the parent set.

In general:

A is a subset of B if and just if every element of A is in B.

So let'southward use this definition in some examples.

Instance: Is A a subset of B, where A = {ane, 3, 4} and B = {i, 4, 3, 2}?

1 is in A, and 1 is in B as well. So far so expert.

3 is in A and iii is also in B.

4 is in A, and 4 is in B.

That'southward all the elements of A, and every single 1 is in B, and so we're done.

Aye, A is a subset of B

Note that 2 is in B, but two is not in A. But remember, that doesn't matter, we only wait at the elements in A.

Let'south endeavour a harder example.

Example: Let A be all multiples of iv and B exist all multiples of 2.
Is A a subset of B? And is B a subset of A?

Well, nosotros can't cheque every element in these sets, because they have an infinite number of elements. And so we need to get an idea of what the elements look similar in each, and then compare them.

The sets are:

  • A = {..., −8, −4, 0, 4, viii, ...}
  • B = {..., −8, −6, −iv, −2, 0, 2, 4, 6, 8, ...}

By pairing off members of the two sets, we can see that every member of A is also a member of B, simply non every member of B is a member of A:

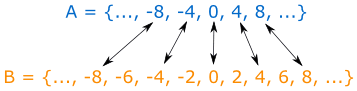
pairing off A and B

So:

A is a subset of B, but B is not a subset of A

Proper Subsets

If nosotros await at the defintion of subsets and permit our mind wander a bit, we come to a weird determination.

Let A be a gear up. Is every element of A in A?

Well, umm, yeah of course, right?

And so that means that A is a subset of A . It is a subset of itself!

This doesn't seem very proper, does it? If we desire our subsets to be proper we introduce (what else but) proper subsets:

A is a proper subset of B if and only if every element of A is also in B, and there exists at least i element in B that is not in A.

This little piece at the end is at that place to make sure that A is not a proper subset of itself: we say that B must have at least one extra element.

Example:

{1, 2, 3} is a subset of {ane, ii, iii}, but is non a proper subset of {1, two, three}.

Instance:

{ane, ii, three} is a proper subset of {1, 2, 3, 4} because the element four is not in the offset set up.

Find that when A is a proper subset of B then it is too a subset of B.

Fifty-fifty More Annotation

When we say that A is a subset of B, we write A subset symbol B.

Or we tin can say that A is non a subset of B past A not subset symbol B ("A is not a subset of B")

When nosotros talk near proper subsets, we take out the line underneath and then it becomes A proper subset symbol B or if we desire to say the opposite, A not proper subset symbol B.

Empty (or Cypher) Gear up

This is probably the weirdest thing about sets.

keys on guitar

Every bit an case, think of the ready of piano keys on a guitar.

"But wait!" y'all say, "At that place are no piano keys on a guitar!"

And correct you are. It is a prepare with no elements.

This is known as the Empty Set (or Null Set).There aren't any elements in it. Not one. Zero.

Information technology is represented by null set

Or past {} (a set with no elements)

Another examples of the empty set are the set of countries south of the s pole.

So what's so weird about the empty set? Well, that part comes adjacent.

Empty Set and Subsets

And so let'south go dorsum to our definition of subsets. We have a prepare A. We won't define it any more that, information technology could exist any set. Is the empty set a subset of A?

Going back to our definition of subsets, if every element in the empty set is also in A, then the empty set is a subset of A. But what if we accept no elements?

It takes an introduction to logic to understand this, just this argument is one that is "vacuously" or "trivially" true.

A skillful way to think about it is: nosotros can't find whatsoever elements in the empty set that aren't in A, so it must exist that all elements in the empty set are in A.

So the answer to the posed question is a resounding yes.

The empty fix is a subset of every ready, including the empty prepare itself.

Order

No, not the order of the elements. In sets it does non affair what order the elements are in.

Instance: {1,2,3,4} is the same fix as {3,1,4,ii}

When we say order in sets we mean the size of the prepare.

Another (meliorate) name for this is cardinality.

A finite prepare has finite lodge (or cardinality). An infinite gear up has space order (or cardinality).

For finite sets the order (or cardinality) is the number of elements.

Example: {10, xx, xxx, 40} has an guild of 4.

For infinite sets, all we can say is that the lodge is space. Oddly enough, nosotros can say with sets that some infinities are larger than others, but this is a more advanced topic in sets.

Arg! Not more than notation!

Nah, just kidding. No more notation.

by

Ricky Shadrach

and

Rod Pierce